CheerUp_Cheers
알고리즘 정렬기본 본문
- 안정정렬?
- 알고리즘이란?
- 정렬 알고리즘 시간 복잡도 비교
- 삽입정렬
- 선택정렬
- 쉘정렬
- 버블정렬
- 퀵정렬
- 힙정렬
- 병합정렬
-
안정정렬?
안정정렬은 동일한 값에 대해 기존의 순서가 유지되는 정렬을 말하며 불안정정렬은 반대로 동일한 값에 대해 기존의 순서가 뒤바뀔 수 있는 정렬입니다.
-
알고리즘이란?
- 문제를 해결하기 위해 사용하는 방식
- 같은 문제라도 여러 알고리즘이 존재.
- 알고리즘을 생각할때는 효율도 같이 생각해야 함.
-
-
정렬 알고리즘 시간 복잡도 비교

- 셀 정렬 최악 : 오름차순으로 정렬해야하는데 내림차순으로 되어 있을 경우.
- 퀵 정렬 최악 : 데이터 배열이 역순일 경우 최악의 경우.
- O(N)
실행시간(1억일경우, 10^8) - 0.1s
카운팅
- O(NLogN)
실행시간(1억일경우, 10^8) - 2.66s
힙,쉘,병합,퀵
- O(N^2)
실행시간(1억일 경우, 10^8) -1157.days
삽입,선택 거품
-
삽입정렬
- 정의
(자기보다) 작은 수가 나올 때까지 우로 밀어 삽입하는 정렬
정렬은 2번쨰 원소부터 시작, 그 앞의 원소들과 비교하여 삽입할 위치를 지정후, 뒤의 원소를 옮기고 지정된 자리에 삽입.
- 시간복잡도 : O(N^2), 최선의 경우 O(N)
- 안정성 : 일반적으로 있음.
- 장점
1) 대부분의 원소가 이미 정렬되어 있으면 매우 효율적
2) 다른 메모리 공간 필없음 => 제자리 정렬
3) 안정 정렬
- 단점
버블이나 선택처럼 배열의 길이가 길어질수록 비효율적.

-
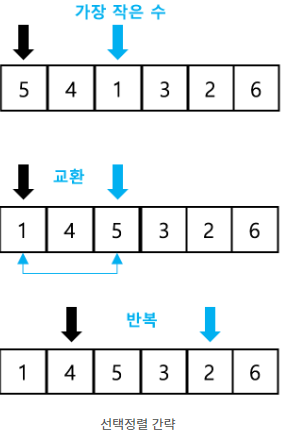
선택정렬
- 정의
(순차적으로) 가장 작은 수를 선택하고 (반복) 교환하는 정렬
해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 그 자리에 올값 찾는 것.
- 시간 복잡도
O(N^2), N-1 + N-2 + 1... => n(n-1)/2 => N^2
- 안정성 : 없음
- 장점
1) 버블 정렬에 비해 실제로 교환하는 적어서 많은 교환이일어나는 자료상태에서 비교적효율.
2) 다른 메모리공간 필 없음(제자리 정렬)
- 단점
1) 불안정 정렬
-
거품정렬
- 정의 : 좌측 값이 자기 보다 크면 교환하는 정렬
- 시간 복잡도 : O(N^2)
n-1 + n-2... + 1 => n(n-1)/2 => N^2
- 안정성 : 일반적으로 있음(안정 절렬)
- 장점
1) 구현간단, 직관적
2) 정렬하고자하는 배열의 교환, 다른 메모리공간 필없음(제자리 정렬)
3) 안정 정렬
- 단점
1) 시간복잡도가 최악,최선,평균이 모두같아서 비효율
2) 정렬돼있찌 않은 원소가 정렬된 자리로 가기위해 교환연산이 많이 일어남.

-
쉘 정렬
정의 : (자기 보다) 작은수가 나올때 까지 간격만큼 우로 민다.(삽입정렬)
시간 복잡도 : 평균 O(N^1.5), 최악 O(N^2)
안전성 : 없음

-
퀵 정렬
- 정의
좌측, 우측 값을 축 값과 비교하고 교환후 (재귀적) 분할하는 정렬
분할 정복, 배열 가운데 하나의 원소를 고르고 피벗(자리안바뀜) 앞에는 작은거 뒤에는 큰거로 분할
분할된 작은 영역에대해 재귀적 과정
- 시간 복잡도 :
O(log2N), O(NlogN)
최악의 경우 : 오름차순이거나 내림차순 정렬일 경우 O(N^2) => 분할이 나누어지지 않아..
- 안정성 : 없음
- 장점
1) 한번 결정된 피벗들이 추후 연산에서 제외되어 빠름
2) 다른 메모리 공간 필요없음(정렬하고자하는 배열안에서 교환)
- 단점
1) 불안정 정렬
2) 정렬된 상태에서는 불균형 분할로 오히려 수행시간 뻇음
- 순서
1) 좌측 값이 '축'값 보다 크거나 같은것을 찾을떄까지 비교.
2) 우측 값이 '축'값 보다 작거나 같은것을 찾을떄까지 비교.
3) 좌측값과 우측값을 교환.
4) 좌측 인덱스가 우측 인덱스 보다 크면 배열을 분할.
5) 재귀 반복

-
힙 정렬
- 정의
우선순위 큐를 이용, 다운 힙 , 업 힙 연산으로 정렬
완전 이진 트리르 기본으로 하는 힙 자료구조 기반.
삽입할떄 왼쪽부터 차례대로 추가하는 이진트리.
- 시간 복잡도 : O(NlogN)
-> 힙트리의 전체 높이가 거의 log2n(완전 이진트리) 이니, 하나의 요소를 힙에 삽입하거나 삭제시 log2n
요소의 개수가 n개임으로 전체적으로 O(nlog2n)
- 안정성 : 동일한 값에 대한 기준이 별도로 있어야한다. 또는 동일한 값의 존재를 부정.(불안정)
- 최대 힙 : 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- 순서
1) 최대 힙 루트의 최대값을 마지막요소와 바꾼후, 힙사이즈 줄임
2) 큰거 추출
3) 정렬
4) 힙사이즈가 1보다 크면 계쏙 반복
-
병합 정렬(합병정렬)
- 정의
(최소 단위까지) 배열을 (재귀적으로) 분할 후, 병합 시 (부분 배열의) 앞에서 부터 비교 삽입 하는 정렬.
쪼개는 방식은 퀵정렬과 유사(분할정복)
차이점
퀵정렬 : 피벗을 통해 정렬 -> 영역을 쪼갬
합병 : 영역을 쪼갤수있을만금 쪼갬 -> 정렬
- 시간 복잡도 : 모두 O(NlogN)
- 안정성 : 안정성이 있다.
- 장점
1) 합병정렬은 순차적인 비교로 정렬을 진행, 링크드리스트의 정렬에 효율
-> 퀵정렬은 순차접근이 아닌 임의접근이라 오버헤드



